Inestigcion matematica.. sabado
Este es la investigación que mando el dia sábado.. ojo sacar resumen de las que están bastante
Combinatoria
La combinatoria es una rama de la matemática perteneciente al área de matemáticas discretas que estudia la enumeración, construcción y existencia de propiedades de configuraciones que satisfacen ciertas condiciones establecidas. Además, estudia las ordenaciones o agrupaciones de un determinado número de elementos.
Entre las subdivisiones más comunes se encuentran las siguientes.
Ésta fue una de las primeras áreas de la combinatoria en ser desarrollada, y como otras áreas más recientes se estudian sólo en cursos especializados, es común que se haga referencia a esta subárea cuando se menciona combinatoria en entornos escolares.
El factorial de un entero positivo n, el factorial de n o n factorial se define en principio como el producto de todos los números enteros positivos desde 1 (es decir, los números naturales) hasta n. Por ejemplo,
La definición de la función factorial también se puede extender a números no naturales manteniendo sus propiedades fundamentales, pero se requieren matemáticas avanzadas, particularmente del análisis matemático.
La notación matemática actual n! fue usada por primera vez en 1808[1] por Christian Kramp (1760–1826), un matemático francés que trabajó en especial sobre los factoriales toda su vida.
La segunda definición incorpora la premisa de que
Una extensión común, sin embargo, es la definición de factorial de cero. De acuerdo con la convención matemática de producto vacío, el valor de 0! debe definirse como:
Así, si se conoce que 5! es 120, entonces 4! es 24 porque
Por ejemplo en la cerradura de arriba, hay 10 números para elegir (0,1,...,9) y eliges 3 de ellos:
Así que tu primera elección tiene 16 posibilidades, y tu siguiente elección tiene 15 posibilidades, después 14, 13, etc. Y el total de permutaciones sería:
¿Pero cómo lo escribimos matemáticamente? Respuesta: usamos la "función factorial"
Así que si quieres elegir todas las bolas de billar las permutaciones serían:
¿Lo ves? 16! / 13! = 16 × 15 × 14
La fórmula se escribe:
¿De cuántas maneras se pueden dar primer y segundo premio entre 10 personas?
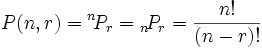



La manera más fácil de explicarlo es:
Ya sabemos que 3 de 16 dan 3360 permutaciones.
Pero muchas de ellas son iguales para nosotros, porque no nos importa el orden.
Por ejemplo, digamos que se tomaron las bolas 1, 2 y 3. Las posibilidades son:
Así que las permutaciones son 6 veces más posibilidades.
De hecho hay una manera fácil de saber de cuántas maneras "1 2 3" se pueden ordenar, y ya la sabemos. La respuesta es:
Así que sólo tenemos que ajustar nuestra fórmula de permutaciones para reducir por las maneras de ordenar los objetos elegidos (porque no nos interesa ordenarlos):
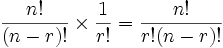 Esta fórmula es tan importante que normalmente se la escribe con grandes paréntesis, así:
Esta fórmula es tan importante que normalmente se la escribe con grandes paréntesis, así:
Y se la llama "coeficiente binomial".
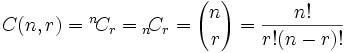 Entonces, nuestro ejemplo de bolas de billar (ahora sin orden) es:
Entonces, nuestro ejemplo de bolas de billar (ahora sin orden) es:
O lo puedes hacer así:
Áreas de la combinatoria
No existe una clasificación tajante de lo que constituye una subárea, sino que todas comparten cierto grado de traslape entre sí, al igual que con otras ramas de la matemática discreta. Diferentes autores proponen varias divisiones de la combinatoria por lo que cualquier listado es meramente indicativo. Por ejemplo, algunos autores consideran la teoría de grafos como una subárea de la combinatoria, mientras que otros la consideran un área independiente.Entre las subdivisiones más comunes se encuentran las siguientes.
Combinatoria enumerativa
La combinatoria enumerativa o enumeración estudia los métodos para contar (enumerar) las distintas configuraciones de los elementos de un conjunto que cumplan ciertos criterios especificados.Ésta fue una de las primeras áreas de la combinatoria en ser desarrollada, y como otras áreas más recientes se estudian sólo en cursos especializados, es común que se haga referencia a esta subárea cuando se menciona combinatoria en entornos escolares.
- Ejemplo.
- Un primer problema podría consistir en hallar el número de formas diferentes en que podemos sacar las tarjetas una después de otra (es decir, el número de permutaciones del conjunto).
- Por ejemplo, dos formas distintas podrían ser: EIAOU o OUAIE.
- Después, se puede preguntar por el número de formas en que se puede sacar sólo 3 tarjetas del sombrero (es decir, el número de 3-permutaciones del conjunto).
- En este caso, ejemplos pueden ser IOU, AEI o EAI.
- También se puede preguntar sobre cuáles son los posibles grupos de 3 tarjetas que se pueden extraer, sin dar consideración al orden en que salen (en otras palabras, el valor de un coeficiente binomial).
- Aquí, consideraríamos AOU y UAO como un mismo resultado.
- Otro problema consiste en hallar el número de formas en que pueden salir 5 tarjetas, una tras otra, pero en cada momento se regresa la tarjeta escogida al sombrero.
- En este problema los resultados posibles podrían ser EIOUO, IAOEU o IEAEE.
Factorial
De Wikipedia, la enciclopedia libre
La definición de la función factorial también se puede extender a números no naturales manteniendo sus propiedades fundamentales, pero se requieren matemáticas avanzadas, particularmente del análisis matemático.
La notación matemática actual n! fue usada por primera vez en 1808[1] por Christian Kramp (1760–1826), un matemático francés que trabajó en especial sobre los factoriales toda su vida.
Definición
La función factorial es formalmente definida mediante el producto- .
- .
La segunda definición incorpora la premisa de que
Cero factorial
La definición indicada de factorial es válida para números positivos. Es posible extender la definición a otros contextos introduciendo conceptos más sofisticados, en especial es posible definirla para cualquier número real excepto para los números enteros negativos y para cualquier número complejo exceptuando de nuevo los números enteros negativos.Una extensión común, sin embargo, es la definición de factorial de cero. De acuerdo con la convención matemática de producto vacío, el valor de 0! debe definirse como:
- Para cada número entero positivo n mayor o igual que 1, es posible determinar el valor del factorial anterior mediante el uso de la siguiente identidad:
Así, si se conoce que 5! es 120, entonces 4! es 24 porque
Permutaciones
Hay dos tipos de permutaciones:- Se permite repetir: como la cerradura de arriba, podría ser "333".
- Sin repetición: por ejemplo los tres primeros en una carrera. No puedes quedar primero y segundo a la vez.
1. Permutaciones con repetición
Son las más fáciles de calcular. Si tienes n cosas para elegir y eliges r de ellas, las permutaciones posibles son:
n × n × ... (r veces) = nr
(Porque hay n posibilidades para la primera elección, DESPUÉS hay n posibilidades para la segunda elección, y así.)Por ejemplo en la cerradura de arriba, hay 10 números para elegir (0,1,...,9) y eliges 3 de ellos:
10 × 10 × ... (3 veces) = 103 = 1000 permutaciones
Así que la fórmula es simplemente:| nr |
| donde n es el número de cosas que puedes elegir, y eliges r de ellas (Se puede repetir, el orden importa) |
2. Permutaciones sin repetición
En este caso, se reduce el número de opciones en cada paso. | Por ejemplo, ¿cómo podrías ordenar 16 bolas de billar? Después de elegir por ejemplo la "14" no puedes elegirla otra vez. |
16 × 15 × 14 × 13 ... = 20,922,789,888,000
Pero a lo mejor no quieres elegirlas todas, sólo 3 de ellas, así que sería solamente:
16 × 15 × 14 = 3360
Es decir, hay 3,360 maneras diferentes de elegir 3 bolas de billar de entre 16.¿Pero cómo lo escribimos matemáticamente? Respuesta: usamos la "función factorial"
 | La función factorial (símbolo: !) significa que se multiplican números descendentes. Ejemplos:
|
| Nota: en general se está de acuerdo en que 0! = 1. Puede que parezca curioso que no multiplicar ningún número dé 1, pero ayuda a simplificar muchas ecuaciones. | |
16! = 20,922,789,888,000
Pero si sólo quieres elegir 3, tienes que dejar de multiplicar después de 14. ¿Cómo lo escribimos? Hay un buen truco... dividimos entre 13!...
16 × 15 × 14 × 13 × 12 ...
| = 16 × 15 × 14 = 3360 | |
13 × 12 ...
|
La fórmula se escribe:
| donde n es el número de cosas que puedes elegir, y eliges r de ellas (No se puede repetir, el orden importa) |
Ejemplos:
Nuestro "ejemplo de elegir en orden 3 bolas de 16" sería:| 16! | = | 16! | = | 20,922,789,888,000 | = 3360 |
| (16-3)! | 13! | 6,227,020,800 |
| 10! | = | 10! | = | 3,628,800 | = 90 |
| (10-2)! | 8! | 40,320 |
(que es lo mismo que: 10 × 9 = 90)
Notación
En lugar de escribir toda la fórmula, la gente usa otras notaciones como:Variaciones
Se llama variaciones ordinarias de m elementos tomados de n en n (m ≥ n) a los distintos grupos formados por n elementos de forma que:
No entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.

También podemos calcular las variaciones mediante factoriales:

Las variaciones se denotan por 

Variaciones con repetición
Se llama variaciones con repetición de m elementos tomados de n en n a los distintos grupos formados por n elementos de manera que:
No entran todos los elementos si m > n. Sí pueden entrar todos los elementos si m ≤ n
Sí importa el orden.
Sí se repiten los elementos.

Combinaciones
También hay dos tipos de combinaciones (recuerda que ahora el orden no importa):- Se puede repetir: como monedas en tu bolsillo (5,5,5,10,10)
- Sin repetición: como números de lotería (2,14,15,27,30,33)
1. Combinaciones con repetición
En realidad son las más difíciles de explicar, así que las dejamos para luego.2. Combinaciones sin repetición
Así funciona la lotería. Los números se eligen de uno en uno, y si tienes los números de la suerte (da igual el orden) ¡entonces has ganado!La manera más fácil de explicarlo es:
- imaginemos que el orden sí importa (permutaciones),
- después lo cambiamos para que el orden no importe.
Ya sabemos que 3 de 16 dan 3360 permutaciones.
Pero muchas de ellas son iguales para nosotros, porque no nos importa el orden.
Por ejemplo, digamos que se tomaron las bolas 1, 2 y 3. Las posibilidades son:
| El orden importa | El orden no importa |
| 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 | 1 2 3 |
De hecho hay una manera fácil de saber de cuántas maneras "1 2 3" se pueden ordenar, y ya la sabemos. La respuesta es:
3! = 3 × 2 × 1 = 6
(Otro ejemplo: 4 cosas se pueden ordenar de 4! = 4 × 3 × 2 × 1 = 24 maneras distintas, ¡prueba tú mismo!)Así que sólo tenemos que ajustar nuestra fórmula de permutaciones para reducir por las maneras de ordenar los objetos elegidos (porque no nos interesa ordenarlos):
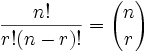 |
| donde n es el número de cosas que puedes elegir, y eliges r de ellas (No se puede repetir, el orden no importa) |
Notación
Además de los "grandes paréntesis", la gente también usa estas notaciones: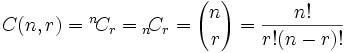
Ejemplo
| 16! | = | 16! | = | 20,922,789,888,000 | = 560 |
| 3!(16-3)! | 3!×13! | 6×6,227,020,800 |
| 16×15×14 | = | 3360 | = 560 |

 . Podemos imaginar que estos elementos corresponden a tarjetas dentro de un sombrero.
. Podemos imaginar que estos elementos corresponden a tarjetas dentro de un sombrero.


 .
. .
.








Comentarios
Publicar un comentario